Những điểm đáng ngờ về lực hấp dẫn – P1: Sự dị thường của trọng lực

Chuyện kể rằng vào năm 1665, một quả táo rơi trúng đầu của Isaac Newton đã khiến ông có ý tưởng về trọng lực. Ông cho rằng lực kéo một quả táo xuống Trái Đất cũng giống như lực giữ Mặt Trăng trên quỹ đạo quay quanh Trái Đất; và sở dĩ Mặt Trăng không rơi xuống Trái Đất là do chuyển động quanh quỹ đạo của nó có tác dụng chống lại lực hấp dẫn. Nếu Mặt Trăng ngừng chuyển động theo quỹ đạo, nó sẽ rơi xuống Trái Đất với gia tốc trọng lực là 9,8m/s² – giống như gia tốc của một quả táo hoặc bất kỳ vật thể nào khác rơi tự do.

Tuy vậy, ngày nay các nhà khoa học đã phát hiện ra nhiều vấn đề mâu thuẫn với định luật hấp dẫn của Newton. Thậm chí có nhiều người cho rằng cái gọi là lực hấp dẫn thực ra không tồn tại. Dưới đây là một số kết quả nghiên cứu của các nhà khoa học về vấn đề này.

Theo định luật vạn vật hấp dẫn của Newton, một vật m sẽ bị kéo về phía vật M với gia tốc trọng trường g = G*M/r² với G là hằng số hấp dẫn và r là khoảng cách giữa 2 vật.

Theo định luật 2 của Newton, vật có khối lượng m chịu lực hấp dẫn có độ lớn F=m*g trong đó g là gia tốc trọng trường (9,8m/s²).

Như vậy, lực hấp dẫn giữa 2 vật được tính như sau: F = G*m*M/r²

Nếu Trái Đất có mật độ không đổi ρ thì tổng khối lượng sẽ là M(r) = (4/3)πρr³ trong đó r là bán kính Trái Đất.

Khi đó, gia tốc trọng trường g ở một nơi có bán kính r sẽ = g(r) = (4/3)*π*G*ρ*r và phụ thuộc vào mật độ của vật chất Trái Đất. (Tạm gọi đây là công thức thứ 4 trong 4 công thức về trọng lực).

Sai số của hằng số hấp dẫn quá lớn

Theo dữ liệu năm 1998 của CODATA (Ủy ban Dữ liệu Khoa học và Công nghệ) do Hội đồng Khoa học Quốc tế thành lập, hằng số hấp dẫn có giá trị = 6,673(10) x 10^-11 m³ kg^-1 s^-2 và có độ chính xác 1,5×10^-3 (1,5 phần nghìn).

Trong khi các giá trị của nhiều hằng số cơ bản, có độ chính xác đến 8 chữ số thập phân (độ chính xác vài phần trăm triệu) thì giá trị của hằng số hấp dẫn đo được trong các thí nghiệm khác nhau khác biệt với nhau từ con số thập phân thứ 3 trở đi, thậm chí có trường hợp khác biệt chỉ là một số sau dấu phẩy, nghĩa là sai số giữa các thí nghiệm lên đến hàng chục phần trăm (%). Điều này quả thật là rất kỳ lạ trong thời đại công nghệ chính xác hiện nay. [1]

Năm 1981, một bài báo đã được xuất bản cho thấy, các phép đo hằng số hấp dẫn G trong các mỏ sâu, lỗ khoan và dưới biển đã cho giá trị cao hơn khoảng 1% so với hiện tại là đã được chấp nhận [2]. Hơn nữa, thí nghiệm ở khu vực càng sâu, sự khác biệt càng lớn.

Hằng số hấp dẫn còn phụ thuộc vào nhiều yếu tố khác?

Một số nhà thí nghiệm trước đó đã phát hiện ra sự bất thường không tương thích với lý thuyết của vật lý trường phái Newton, nhưng kết quả đã bị lãng quên từ lâu.

Chẳng hạn, Charles Brush đã thực hiện các thí nghiệm rất chính xác cho thấy ở cùng một khối lượng (mass – đơn vị đo là kg) trong thí nghiệm, các kim loại có trọng lượng (weight, đơn vị đo là Newton – N) và mật độ nguyên tử rất cao có xu hướng rơi nhanh so với các nguyên tố có trọng lượng (weight) và mật độ nguyên tử thấp hơn.

Ông cũng báo cáo rằng một khối lượng (mass) hoặc số lượng không đổi của một số kim loại có thể thay đổi đáng kể trọng lượng bằng cách thay đổi điều kiện vật lý của nó. [3] Công trình của ông không được cộng đồng khoa học nhìn nhận một cách nghiêm túc và kỹ thuật chụp ảnh tia lửa rất chính xác mà ông sử dụng trong các thí nghiệm rơi tự do chưa bao giờ được các nhà điều tra khác sử dụng. Các thí nghiệm của Victor Crémieu cho thấy lực hấp dẫn đo được trong nước ở bề mặt Trái Đất dường như lớn hơn một phần mười so với kết quả của lý thuyết Newton. [4]

Bất thường bất ngờ tiếp tục xuất hiện. Mikhail Gersteyn đã chỉ ra rằng hằng số hấp dẫn G thay đổi ít nhất 0,054% tùy theo hướng của hai khối lượng (mass) thí nghiệm so với các ngôi sao cố định. [5] Gary Vezzoli đã phát hiện ra rằng cường độ của các tương tác hấp dẫn thay đổi từ 0,04 đến 0,05% như là một hàm số của nhiệt độ, hình dạng và pha của vật thể. [6]

>> Giải mã bí ẩn việc các lạt-ma Tây Tạng nâng tảng đá bằng âm thanh

Các trường vật chất khác cũng ảnh hưởng đến hằng số hấp dẫn?

Donald Kelly đã chứng minh rằng nếu khả năng hấp thụ của vật thể bị giảm bằng cách từ hóa hoặc cung cấp năng lượng cho nó, nó sẽ bị hút vào Trái Đất với tốc độ gia tăng thấp hơn so với gia tốc trọng trường g. [7]

Các nhà vật lý thường đo gia tốc trọng trường g theo một phương pháp có kiểm soát, trong đó không làm thay đổi khả năng hấp thụ của vật thể so với trạng thái thông thường của chúng. Một nhóm các nhà khoa học Nhật Bản đã phát hiện ra rằng một con quay hồi chuyển đang quay phải rơi nhanh hơn một chút so với khi nó không quay. [8]

Bruce DePalma phát hiện ra rằng các vật thể quay rơi trong từ trường tăng tốc nhanh hơn gia tốc trọng trường g. [9]

Phân bố trọng lực trên Trái Đất không như lý thuyết dự đoán

Các nhà khoa học đã chỉ ra rằng phân bố mật độ vật chất trên Trái Đất là không đồng đều nhau. Theo đó, phần lõi chính của Trái Đất (bán kính khoảng 1000km) có mật độ lớn nhất và giảm dần từ tâm Trái Đất ra đến bề mặt Trái Đất và đại dương.

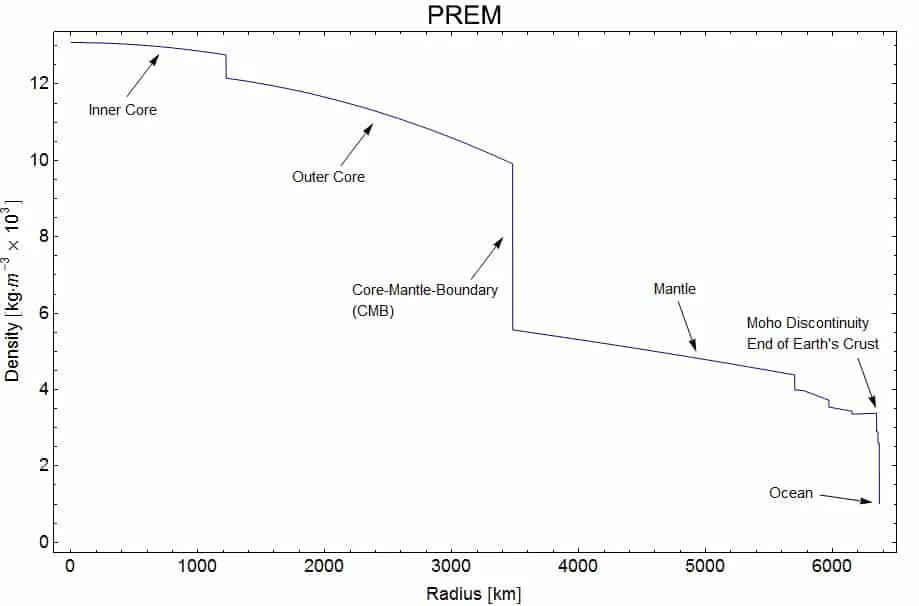
Công thức thứ 4 ở trên đã chỉ ra rằng trọng lực (hay gia tốc trọng trường) ở các vị trí khác nhau trên Trái Đất sẽ thay đổi tùy theo phân bố mật độ xuyên tâm của Trái Đất.

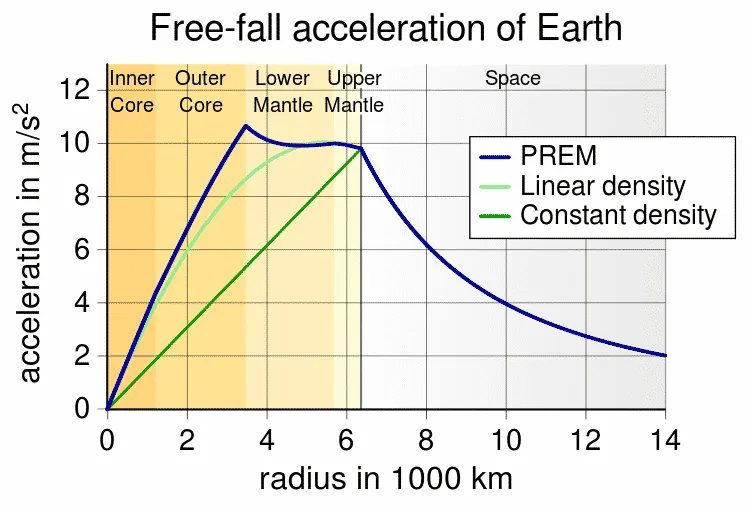
Tuy vật, như đã đề cập ở trên, các phép đo trọng lực bên dưới bề mặt Trái Đất luôn cao hơn dự đoán theo lý thuyết Newton. [10] Những người hoài nghi chỉ đơn giản cho rằng điều này sẽ xuất hiện ở các loại đá có mật độ cao bất thường nằm dưới bề mặt Trái Đất. Tuy nhiên, các phép đo trong các mỏ có mật độ biết trước, đã cho kết quả dị thường tương tự, ví dụ như các phép đo ở độ sâu 1673 mét trong một tảng băng đồng nhất ở Greenland, ngay trên lớp đá vỏ Trái Đất.

Harold Aspden chỉ ra rằng trong một số thí nghiệm, các vỏ bọc kiểu lồng Faraday được đặt xung quanh hai quả cầu kim loại nhằm ngăn chặn các nhiễu điện từ trường từ bên ngoài. Ông lập luận rằng điều này có thể dẫn đến việc tích điện và giữ trên các quả cầu, do đó có thể tạo ra spin chân không (hay đúng hơn là ether), một luồng năng lượng ether tỏa ra dưới dạng nhiệt lượng dư thừa, dẫn đến thay đổi giá trị của hằng số hấp dẫn trong phép đo. [11]

Trên cơ sở trọng lực của Newton, có thể dự kiến ​​rằng lực hấp dẫn trên các lục địa, và đặc biệt là các ngọn núi, sẽ cao hơn so với các đại dương. Trong thực tế, trọng lực trên đỉnh của những ngọn núi lớn lại thấp hơn mong đợi dựa trên cơ sở khối lượng có thể nhìn thấy của chúng. Trong khi đó trên bề mặt đại dương, trọng lực lại cao đến không ngờ.

Để giải thích điều này, khái niệm đẳng tĩnh đã được phát triển: người ta cho rằng các lớp đá có mật độ thấp tồn tại ở độ cao 30 đến 100km dưới các ngọn núi, làm nổi khiến trọng lực ở đây thấp, trong khi các lớp đá có mật độ lớn hơn tồn tại ở độ sâu 30 đến 100km dưới đáy đại dương. Tuy nhiên, giả thuyết này còn lâu mới được chứng minh. Nhà vật lý Maurice Allais nhận xét: “Có sự vượt quá trọng lực trên đại dương và sự thiếu hụt trên các lục địa. Lý thuyết đẳng tĩnh chỉ cung cấp một lời giải thích giả lập cho điều này”. [12]

Lý thuyết tiêu chuẩn, đơn giản về đẳng tĩnh mâu thuẫn với thực tế là trong các vùng hoạt động kiến ​​tạo, các chuyển động thẳng đứng thường tăng cường các trọng lực dị thường, cụ thể là làm mật độ tăng lên hơn là khôi phục lại trạng thái cân bằng đẳng tĩnh.

>> Sự hình thành vũ trụ: Phải chăng Kinh thánh và khoa học tương đồng?

 Thách thức đến từ quỹ đạo xa xôi của các hành tinh

Thuyết hấp dẫn của Newton còn bị thách thức bởi sự phân bố của các hành tinh. [13]

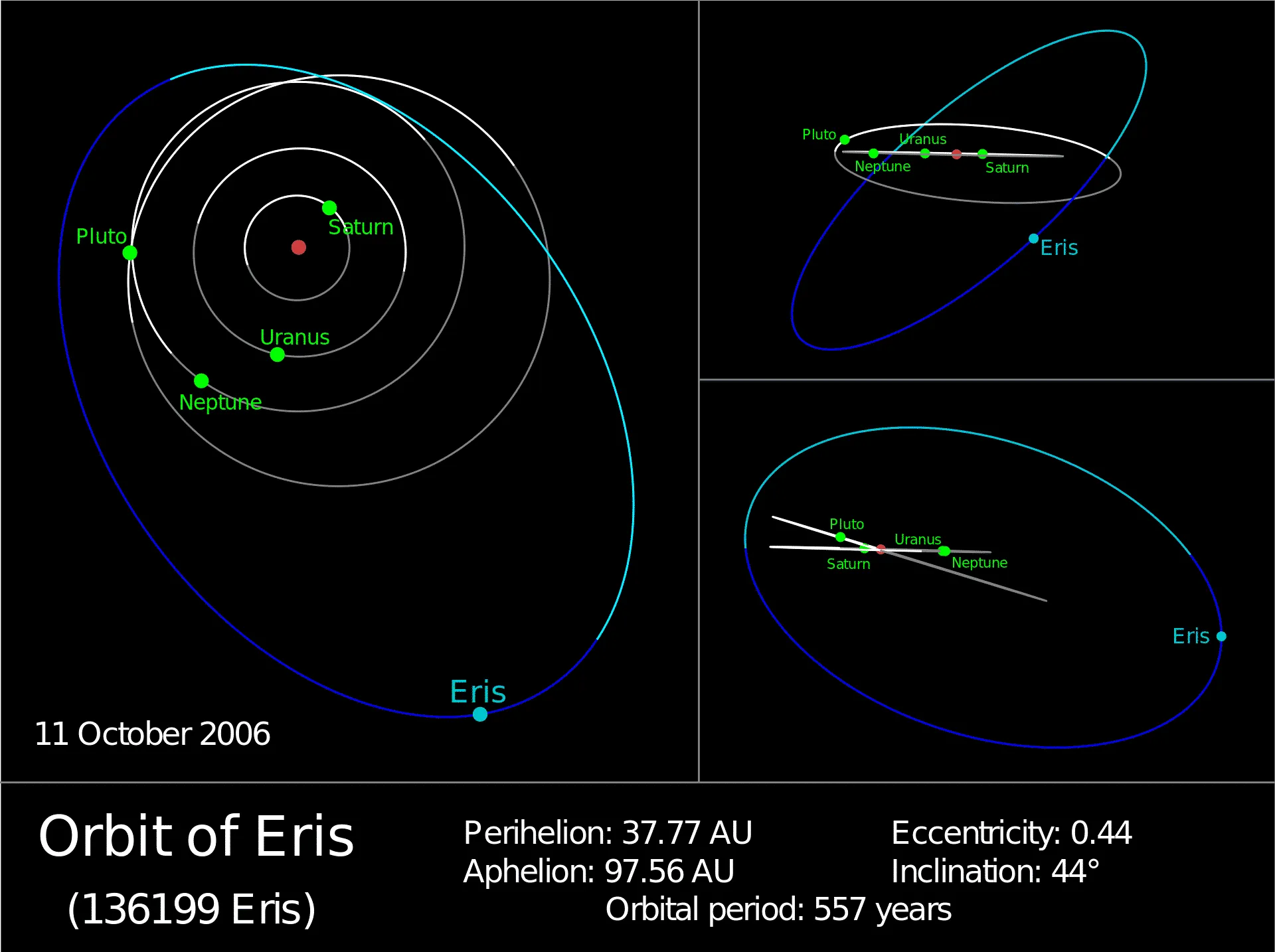
Năm 2005, sau nhiều lần đo đạc và kiểm định, các nhà thiên văn học tuyên bố về việc phát hiện một hành tinh mới quay quanh Mặt Trời. Hành tinh này được gọi là hành tinh lùn, nó được gọi là Eris và có tên khoa học là 2003 UB₃₁₃. Eris nằm ở vị trí ngoài cùng, xa Mặt Trời nhất so với bất cứ hành tinh nào trong hệ Mặt Trời, nó còn vượt ra khỏi vị trí của sao Diêm Vương.

Theo thuyết hấp dẫn của Newton, một hành tinh X, muốn vượt ra ngoài Sao Diêm Vương và quay xung quanh Mặt Trời, thì nó cần phải lớn gấp 2-5 lần so với Trái Đất và cách Mặt Trời hơn 50 đến 100 lần so với Trái Đất. [14] Trái Đất có khối lượng 5.973,6 × 10²¹ kg và cách Mặt Trời trung bình 1,496*10⁸ km.

Tuy vậy, hành tinh Eris lại chỉ có khối lượng tương đương 0,28% khối lượng Trái Đất; quỹ đạo của nó so với Mặt Trời có điểm cực cận và cực viễn lần lượt là 5.723×10⁹km và 14.602×10⁹ km. Nghĩa là, Eris xa Mặt Trời hơn Trái Đất Từ 50 đến 100 lần, nhưng trọng lượng của nó lại nhỏ hơn Trái Đất 36 lần. Rõ ràng, trọng lượng của nó không đáp ứng được lý thuyết của Newton để có đủ lực hấp dẫn từ Mặt Trời và quay quanh Mặt Trời.

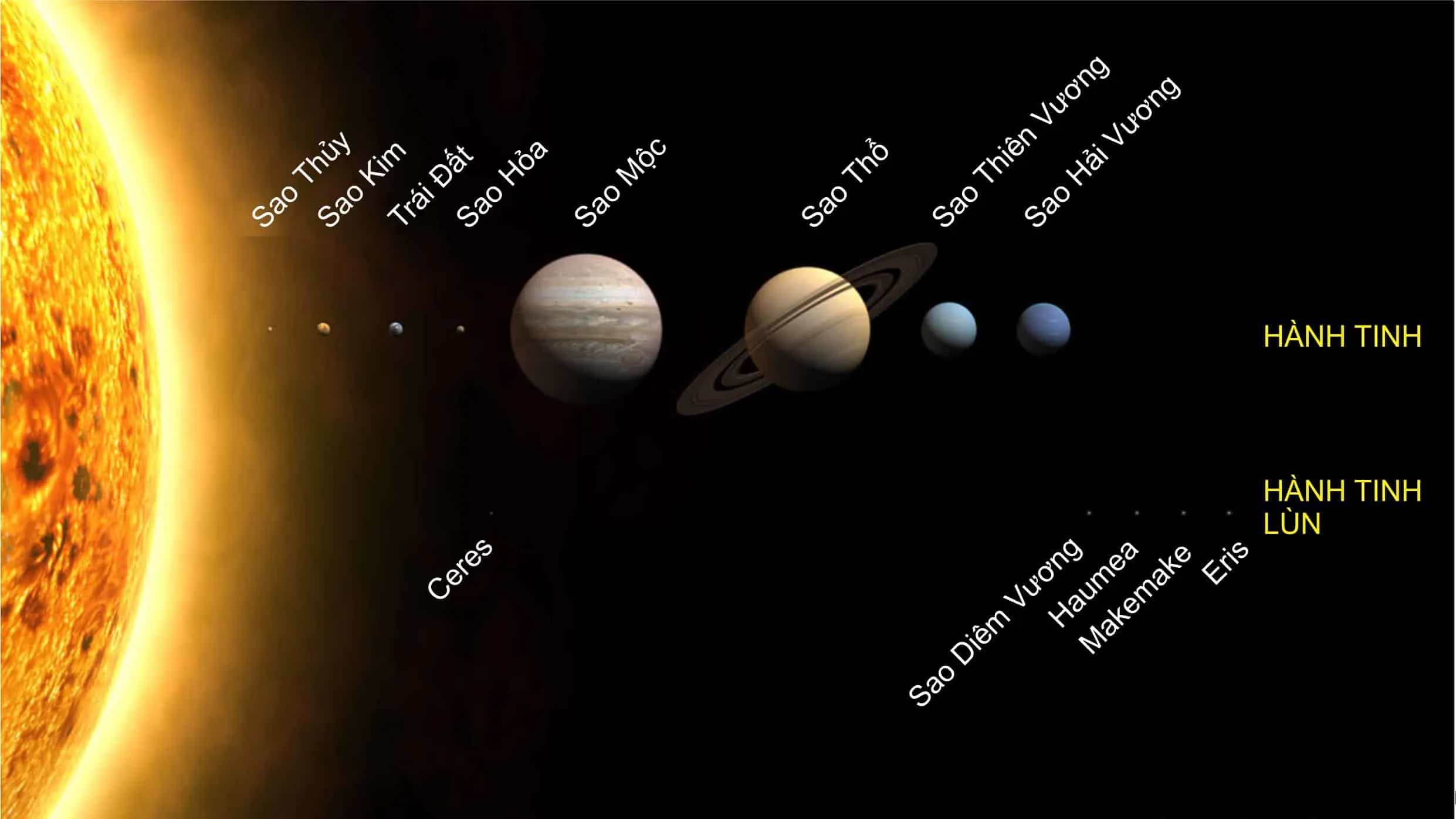
Ngoài hành tinh lùn Eris, các nhà thiên văn học khác cũng phát hiện được 2 hành tinh lùn khác là Haumea và Makemake. Cả hai hành tinh này đều có khối lượng nhỏ hơn Trái Đất hơn 1.000 lần và cách xa Mặt Trời hơn Trái Đất 30-50 lần. Chiểu theo thuyết hấp dẫn của Newton thì cũng không lý giải được vì sao chúng vẫn có thể quay quanh Mặt Trời. [15]

Xem tiếp: Những điểm đáng ngờ về lực hấp dẫn – P2: Trọng lực có thể bị che chắn?

Theo “Gravity and Antigravity” của David Pratt
Thiện Tâm lược dịch và chú giải

Tài liệu tham khảo

[1].     D. Kestenbaum, ‘The legend of G’, New Scientist, 17 Jan 1998, pp. 39-42; Vincent Kiernan, ‘Gravitational constant is up in the air’, New Scientist, 26 Apr 1995, p. 18.

[2].     F.D. Stacey and G.J. Tuck, ‘Geophysical evidence for non-newtonian gravity’, Nature, v. 292, 1981, pp. 230-232.

[3].     Charles F. Brush, ‘Some new experiments in gravitation’, Proceedings of the American Philosophy Society, v. 63, 1924, pp. 57-61.

[4].     Victor Crémieu, ‘Recherches sur la gravitation’, Comptes Rendus de l’académie des Sciences, Dec 1906, pp. 887-889; Victor Crémieu, ‘Le problème de la gravitation’, Rev. Gen. Sc. Pur. et Appl., v. 18, 1907, pp. 7-13.

[5].     Mikhail L. Gershteyn, Lev I. Gershteyn, Arkady Gershteyn, and Oleg V. Karagioz, ‘Experimental evidence that the gravitational constant varies with orientation’, Infinite Energy, 10:55, 2004, pp. 26-28.

[6].     G.C. Vezzoli, ‘Materials properties of water related to electrical and gravitational interactions’, Infinite Energy, 8:44, 2002, pp. 58-63.

[7].     Stephen Mooney, ‘From the cause of gravity to the revolution of science’, Apeiron, 6:1-2, 1999, pp. 138-141; Josef Hasslberger, ‘Comments on gravity drop tests performed by Donald A. Kelly’, Nexus, Dec 1994-Jan 1995, pp. 48-49.

[8].     H. Hayasaka et al., ‘Possibility for the existence of anti-gravity: evidence from a free-fall experiment using a spinning gyro’, Speculations in Science and Technology, v. 20, 1997, pp. 173-181; keelynet.com/gravity/gyroag.htm.

[9].     The Home of Primordial Energy (Bruce DePalma), www.depalma.pair.com; Jeane Manning, The Coming Energy Revolution: The search for free energy, NY: Avery, 1996, pp. 82-86.

[10].     S.C. Holding and G.J. Tuck, ‘A new mine determination of the newtonian gravitational constant’, Nature, v. 307, 1984, pp. 714-716; Mark A. Zumberge et al., ‘Results from the 1987 Greenland G experiment’, Eos, v. 69, 1988, p. 1046; R. Poole, ‘ “Fifth force” update: more tests needed’, Science, v. 242, 1988, p. 1499; Ian Anderson, ‘Icy tests provide firmer evidence for a fifth force’, New Scientist, 11 Aug 1988, p. 29.

[11].     Harold Aspden, ‘Gravity and its thermal anomaly’, Infinite Energy, 7:41, 2002, pp. 61-65.

[12].     M.F.C. Allais, ‘Should the laws of gravitation be reconsidered?’, part 2, Aero/Space Engineering, v. 18, Oct 1959, p. 52.

[13].     W.R. Corliss (comp.), The Moon and the Planets, Glen Arm, MD: Sourcebook Project, 1985, pp. 282-284.

[14].     Tom Van Flandern, Dark Matter, Missing Planets & New Comets, Berkeley, CA: North Atlantic Books, 1993, pp. 315-325.